Solving 2nd Degree Equations
Second degree equations equations are equations that have an x2 term as its
highest power. They
are also called Quadratic equations.
Zero Factor Rule
The zero product rule says
if you have two terms whose product (factors) equal zero then
either the first factor is equal to zero
or the second factor is equal to zero
This rule helps us solve equations that have products (factors) that are
equal
to zero.
(x − 3)(x + 4) = 0
(x + 2)(x − 2) = 0
(4x)(x − 6) = 0
x(5x + 2) = 0
If the polynomial is a second degree equation then the polynomial will have
exactly two factors. If
the product of the two factors equals zero you can use the Zero Product Rule to
find the two
numbers that are solutions to the second degree equation.
Solving 2nd Degree Equations
Step 1: Be sure that the problem has an equation with two factors whose product
is zero.
Step 2: Set each factor with an x term equal to zero. This will give you two
separate equations.
Step 3: Solve each equation separately. The 2 numbers are both solutions to the
original equation.
Step 4: You can check the 2 solutions by substituting either of the numbers into
the original equation
and checking to see that they make original make the equation true.
| Solve each equation. |
| Example 1 |
Example 2 |
| (x −5)(x + 6) = 0 |
(4x)(x − 2) = 0 |
| then |
then |
| x −5 = 0 or x + 6 = 0 |
4x = 0 or x − 2 = 0 |
and solving each
equation for x gives |
and solving each
equation for x gives |
| x = 5 or x = −6 |
x = 0 or x = 2 |
| Check x = 5 |
Check x = −6 |
Check x = 0 |
Check x = 2 |
(5 −5)(5 + 6) = 0
(0)(11) = 0 |
(−6 − 5)(−6+ 6 ) = 0
(−6 −5)(−6 + 6) = 0 |
(4 • 0)(0 − 2) = 0
(0)(−2) = 0 |
(4 • 2)(2 − 2) = 0(8)(0) = 0 |
Both x = 5 and x = 6 are
solutions to |
Both x = 0 and x = 2 are
solutions to |
| (x − 5)(x + 6) = 0 |
(4x)(x −2) = 0 |
Standard Form of a Second Degree Equation
The standard form of a second degree equation requires the x2 term to
be written first and be
positive. The x term is written second and the constant term is written last.
That expression is set
equal to 0.
Standard Form Examples

Solving a Second Degree Equation
If we factor a quadratic equation in standard form we get two factors that have
a product of zero.
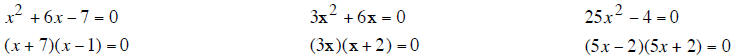
If we then Use the Zero Factor rule we can solve each of
these equations.
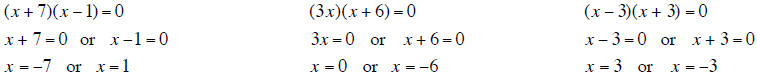
Both numbers are solutions to the original second degree
equation.
To Solve a Second Degree Equation for x:
Step 1: Get the terms in Standard Form and set equal to zero.
Step 2. Factor (Factor out the GCF, The Difference of 2 Perfect Squares, Easy
Trinomials)
Step 3. Set each factor that has an x term equal to zero.
Step 4. Solve each equation for x. Remember that second degree equations have 2
solutions.
| Example 1
|
Example 2 |
Example 3 |
| Solve 6x2 −12x = 0 |
Solve 10x2 + 5x = 0 |
Solve x2 −9 = 0 |
| 6x(x − 2) = 0 |
5x (2x +1) = 0 |
(x − 3) (x + 3) = 0 |
| Set each factor = to 0 |
Set each factor = to 0 |
Set each factor = to 0 |
| 6x = 0 x −2 = 0 |
5x = 0 2x +1 = 0 |
x − 3 = 0 x + 3 = 0 |
| Solve each equation for x |
Solve each equation for x |
Solve each equation for x |
| x = 0 or x = 2 |
x = 0 or
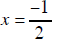 |
x = 3 or x = −3 |
Both numbers are solutions to the original second degree
equation.
| Example 4
|
Example 5 |
Example 6 |
| Solve 4x2 −25 = 0 |
Solve 8x2 − 32 = 0 |
Solve x2 + 8x +15 = 0 |
| (2x −5) (2x + 5) = 0 |
8(x2 − 4) = 0
8(x −2) (x + 2) = 0 |
(x + 5) (x + 3) = 0 |
| Set each factor = to 0 |
Set each factor with an x term =
to 0 |
Set each factor = to 0 |
| 2x −5 = 0 2x + 5 = 0 |
x − 2 = 0 x + 2 = 0 |
x + 5 = 0 x + 3 = 0 |
| Solve each equation for x |
Solve each equation for x |
Solve each equation for x |
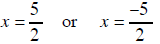 |
x = 2 or x = −2 |
x = −5 or x = −3 |
| Example 7
|
Example 8 |
Example 9 |
| Solve x2 −6x − 7 = 0 |
Solve 6x2 + 7x − 3 = 0 |
Solve 3x2 − 2x − 4 = 0 |
| (x − 7) (x +1) = 0 |
(3x −1) (2x + 3) = 0 |
(x −2) (3x + 4) = 0 |
| Set each factor = to 0 |
Set each factor = to 0 |
Set each factor = to 0 |
| x − 7 = 0 x +1 = 0 |
3x −1 = 0 2x + 3 = 0 |
x −2 = 0 3x + 4 = 0 |
| Solve each equation for x |
Solve each equation for x |
Solve each equation for x |
| x = 7 or x = −1 |
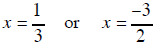 |
x = 2 or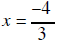 |
| Example 10
|
Example 11 |
Example 12 |
| Solve 8x2 = 4 x |
Solve 16x2 = 81 |
Solve x2 = −9x −14 |
| Put in standard form |
Put in standard form |
Put in standard form |
| 8x2 − 4 x = 0 |
16x2 − 81= 0 |
x2 + 9x +14 = 0 |
| factor 8x2 − 4 x = 0 |
factor 16x2 −81 = 0 |
factor x2 + 9x +14 = 0 |
| 4x(2x −1) = 0 |
(4x −9) (4 x + 9) = 0 |
(x + 7) (x + 2) = 0 |
| Set each factor = to 0 |
Set each factor = to 0 |
Set each factor = to 0 |
| 4x = 0 2x −1= 0 |
4x −9 = 0 4x + 9 = 0 |
x + 7 = 0 x + 2 = 0 |
| Solve each equation for x |
Solve each equation for x |
Solve each equation for x |
| x = 0 or x =1/2 |
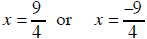 |
x = −7 or x = −2 |
| Example 7
|
Example 8 |
Example 9 |
| Solve 8x2 = 4 x |
Solve 4x2 = 25 |
Solve x2 = −9x −14 |
| Put in standard form |
Put in standard form |
Put in standard form |
| 8x2 − 4 x = 0 |
4x2 −25 = 0 |
x2 + 9x +14 = 0 |
| factor 8x2 − 4 x = 0 |
factor 4x2 −25 = 0 |
factor x2 + 9x +14 = 0 |
| 4x(2x −1) = 0 |
(2x −5) (2x + 5) = 0 |
(x + 7) (x + 2) = 0 |
| Set each factor = to 0 |
Set each factor = to 0 |
Set each factor = to 0 |
| 4x = 0 2x −1= 0 |
2x −5 = 0 2x + 5 = 0 |
x + 7 = 0 x + 2 = 0 |
| Solve each equation for x |
Solve each equation for x |
Solve each equation for x |
| x = 0 or x =1/2 |
x = 5/2 or x = −5/2 |
x = −7 or x = −2 |
|