Solving Equations
Honors Geometry – This packet is due on the first day of
class.
There will be a quiz on the first day of class on this material. If you have any
questions as you work on this packet, please email the Geometry Honors lead
teacher,(I may not answer right away in July). This packet is worth 30 points
(same as quiz).
A. Simplify

3. -52
4. (-5) 2
5. (2+3) • 4 – 5
6. 2 + 3 • 4 – 5
7. 2 • 3(4 – 5)
8. 2 + 6 ÷ 3 • 2
Solve each equation and inequality for X:
9. 10x = 5
10. 2x – 1 = 3x + 4
11. 2x + 1 = 2x + 3
12. 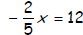
13. 4x = 3(4x – 3)
14. 2x + 4 = 2(x + 2)
15. 7x – (x – 4) = 28
16. 7x = 0
17. 2(x + 5) – 4(x – 5) = 0
18. x + 5 > 10
19. x – 7 > 8 – 2x
20. 6 – x > 2
21. x2 – 25 = 0
22. 3x2 + 3x – 18 = 0
23. x2 + 15 = - 8x
24. 14x2 – 7x = 0
25. (2x – 5)(x + 4) = 0
Using exponents, perform indicated operations and
simplify:
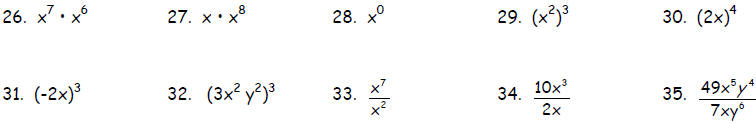
Solve each equation for y, then determine the slope and
the y-intercept:
36. 2y = 2x – 4
37. 7y = 14
38. 3x – 5y = 15
Find the slope and y-intercept of each:
39.
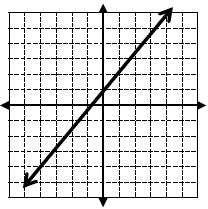
40. y = 2x - 4
41. Find the slope of the line contain the points (-2, 4) and (5, 3)
42. Evaluate the expression x2 - 2x + 5 when x = -3
B. Fill in each blank
1. The origin is the point whose coordinates are
_________________.
2. The coefficient in -7x2 is _____________.
3. The exponent in -7x2 is _____________.
4. The base in 2(x + y)2 is _____________.
5. A polynomial of one term is called a ___________________.
6. A polynomial of two terms is called a ___________________.
7. A polynomial of three terms is called a ___________________.
8. An example of a perfect square trinomial is ______________________.
9. An example of the difference of two squares is ___________________.
10. The solution of the equation x + 2 = x + 3 is _____________________.
11. If a system of equations graph as two parallel lines, the solution is
__________________.
12. If two equation in a system graph as the same line, the solutions are
_________________
and there are ___________ solutions.
13. If two equation in a system graph to form two intersecting lines which
intersect at the
point (1, -5), the solution is _________________ and there is/are _________
solution(s).
14. The slope of a vertical line is _____________________.
15. The slope of a horizontal line is ___________________.
16. The radicand in 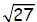 is _________________. is _________________.
17. The coefficient in 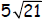 is ______________. is ______________.
C. Practice with multiple choice questions
18. Solve: 3x2 + 5x – 2 = 0
a. x = 1 or x = -2
b. x = -1/3 or x = -2
c. x = 1/3 or x = -2
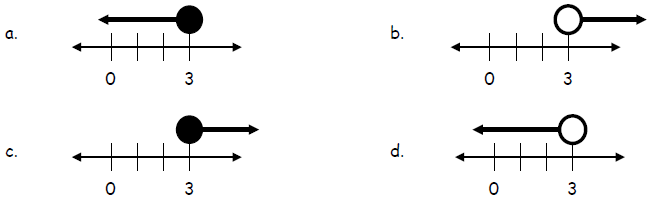
19. Choose the correct graph of 7x – 3(x+ 5) < -3
20. Choose the system for which (5, -1) is the solution:
a. x = -1
y = 5
b. x + 2y = 9
y = -1
c. x – y = 6
x + y = 4
d. 2x + y = 9
x – 3y = 5
21. Multiply: (7x2)(-3x)
a. -10x
b. -21x3
c. -21x4
d. 73(-3) x3 x
22. Simplify: (-2x3) 2
a. 4x6
b. -2x6
c. 4x5
d. -4x6
23. Multiply: (2x – 3)(x + 7)
a. 2x2 - 21
b. 13x – 21
c. 2x2 + 11x – 21
d. 2x2 – 11x + 21
24. Factor completely: 16y - y3
a. y(16 – y2)
b. y(8 - y)(8 + y)
c. y(4 - y)(4 + y)
25. Find the value of a2bc3 when a = -1 , b = 2 , c = -3
a. 54
b. -18
c. 18
d. -54
26. Find the value of 24 ÷ 8 • 3
a. 9
b. 1
c. 1/9
d. 6
27. Use A = ½h(b + c) to find A when h = 8 , b = 7 , and c
= -3
a. 20
b. 16
c. 40
d. 12½
28. Solve: x – 2(9 – x) = 3
a. x = -10½
b. x = 0
c. x = -13
d. x = 7
29. The length of a rectangle is 12 meters more than its
width. Its perimeter is 48 meters.
Find the dimensions of the rectangle.
a. L = 30m w = 18m
b. L = 18m w = 6m
c. L = 30m w = 12m
30. Give the slope of the line containing points (-3, 2)
and (6, -5)
a. -1
b. 1
c. -7/9
d. -9/7
|